Les quadrilatères sont présents partout autour de nous, et pas seulement dans un devoir de mathématique! Qu’est-ce qui les définit? Quels sont les types de quadrilatères? Quelles sont les propriétés spécifiques aux quadrilatères? Pour t’accompagner dans ton apprentissage ou t’aider avec ton devoir, n’hésite pas à faire appel à l’un de nos tuteurs en maths!
Définition d’un quadrilatère en maths
En géométrie, un quadrilatère est un polygone simple qui présente quatre côtés, ainsi que quatre sommets et quatre angles.
Les quadrilatères sont des formes géométriques qui ont quatre côtés. Lorsqu’on trace les diagonales, qui sont les lignes qui relient des sommets opposés, elles se croisent à un point appelé l’intersection des diagonales.
Dans un quadrilatère, on peut mesurer les angles pour voir s’ils sont droits ou aigus. De plus, si on multiplie les longueurs des côtés, on obtient le produit des longueurs, ce qui peut nous aider à comprendre la taille de la forme. Enfin, les sommets d’un quadrilatère, qui sont les points où les côtés se rencontrent, sont très importants pour décrire un quadrilatère !
Les catégories de quadrilatères
La géométrie des quadrilatères révèle de nombreuses propriétés particulières qui les distinguent les unes des autres. Découvrons ensemble les différents quadrilatères existants.
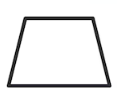
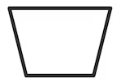
Quadrilatère trapèze
Un trapèze est un quadrilatère qui contient:
- Une paire de côtés parallèles inégaux;
- Diagonales de longueurs différentes;
- Aucune symétrie de réflexion;
- Aucune symétrie de rotation.
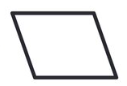
Parallélogramme
Un parallélogramme est un quadrilatère qui contient:
- Deux paires de côtés opposés de même longueur;
- Deux paires de côtés parallèles;
- Deux paires d’angles opposés égaux;
- Diagonales qui se coupent en leurs deux;
- Aucune symétrie de réflexion.
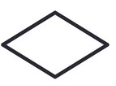
Losange
Un losange est un quadrilatère qui contient:
- Quatre côtés de même longueur;
- Deux paires de côtés parallèles;
- Deux paires d’angles opposés égaux;
- Des diagonales qui se coupent en leur milieu et sont perpendiculaires;
- Deux axes de symétrie.
Carré
Un carré est un quadrilatère qui contient:
- Quatre côtés de même longueur;
- Deux paires de côtés parallèles;
- Quatre angles droits.
- Diagonales de même longueur;
- Diagonales qui se coupent l’une l’autre et sont perpendiculaires;
- Quatre axes de symétrie.
Rectangle
Un rectangle est un quadrilatère qui contient:
- Deux paires de côtés opposés de même longueur;
- Deux paires de côtés parallèles;
- Quatre angles droits;
- Diagonales de même longueur;
- Diagonales qui se coupent en leur milieu;
- Deux axes de symétrie.
Caractéristiques d’un quadrilatère
Les quadrilatères possèdent des caractéristiques propres. Ils ont:
- 4 côtés
- 4 angles (angle droit, angle aigu et/ou angle obtus)
Lexique quadrilatère: polygone convexe
Il existe des quadrilatères convexes sont généralement considérés comme des quadrilatères usuels, soit les plus connus en géométrie.
Un polygone convexe se distingue par l’ensemble de ses mesures des angles internes, qui sont inférieurs à 180 degrés. C’est un type de quadrilatère simple. Par exemple, un rectangle, un carré et un parallélogramme sont des quadrilatères convexes.
Quadrilatère et polygone non convexe
Les quadrilatères non convexes possèdent au moins un angle intérieur supérieur à 180 degrés, ce qui crée une sorte de « creux » dans la forme, comme si elle était repliée vers l’intérieur. Un exemple commun de polygone non convexe est le quadrilatère croisé, où les côtés se chevauchent, n’ayant pas que des segments distincts.
Cette distinction entre un polygone convexe et un polygone non convexe est essentielle pour comprendre les interactions géométriques dans les quadrilatères.
Quadrilatères réguliers et quadrilatères irréguliers
Les quadrilatères réguliers ont tous leurs côtés de la même longueur et tous leurs angles égaux. Le carré est un parfait exemple de quadrilatère régulier.
Les quadrilatères irréguliers n’ont pas cette uniformité et peuvent avoir des longueurs de côtés différentes et des mesures d’angles inégaux.
Quadrilatères particuliers et quadrilatères quelconques
Certains types de polygones et quadrilatères se distinguent des autres par leurs propriétés particulières, comme les parallélogrammes à angles droits, qui présentent des angles droits tout en ayant des côtés opposés de même longueur.
Un quadrilatère orthodiagonal est un autre type particulier de quadrilatère irrégulier où les milieux des diagonales se coupent en angles droits. Tu peux même vérifier la mesure des angles avec un rapporteur d’ angles.
Les quadrilatères inscriptibles possèdent des sommets qui peuvent être placés sur un même cercle, et les quadrilatères bicentriques possèdent des sommets qui peuvent être placés sur un même cercle, de même qu’un cercle qui touche tous les côtés.
Le quadrilatère quelconque, quant à lui, n’est pas un simple polygone à quatre côtés. Ce polygone irrégulier ne suit aucune contrainte particulière. Ces types de quadrilatère sont moins courants.
Le vocabulaire associé aux quadrilatères
Angles et diagonales
La somme des angles intérieurs d’un quadrilatère est en tout temps 360 degrés, ce qui engendre diverses relations et la congruence des angles entre les angles opposés. Les milieux des diagonales sont les lignes qui relient les coins opposés de la forme. Dans certains quadrilatères, les diagonales se croisent à angle droit.
Par exemple, dans un quadrilatère parallélogramme, les angles opposés sont égaux, et les angles adjacents sont complémentaires. L’intersection des diagonales des quadrilatères jouent également un rôle important ; dans un rectangle, elles sont de même longueur et se coupent en leur milieu.
Symétrie et axe de symétrie
La symétrie est un autre aspect essentiel des quadrilatères qui peut être observé à travers ses axes de symétries. Un quadrilatère a des axes de symétrie s’il peut être plié en deux parties identiques. Par exemple, un carré a quatre axes de symétrie tandis que, si l’on regarde les propriétés des rectangles, ils en ont seulement deux.
Les applications pratiques des quadrilatères
La symétrie est un autre aspect essentiel des quadrilatères qui peut être observé à travers ses axes de symétrie. Un quadrilatère a des axes de symétrie s’il peut être plié en deux parties identiques. Par exemple, un carré a quatre axes de symétrie tandis que, si l’on regarde les propriétés des rectangles, ils en ont seulement deux. Ces propriétés peuvent également être étudiées à travers les produits des longueurs de certains segments ou encore en analysant les milieux des diagonales, ce qui permet de mieux comprendre la structure du quadrilatère.
Par ailleurs, le concept d’isobarycentre des sommets s’avère utile, même dans le cas d’un polygone irrégulier. De plus, la manière dont un sommet rencontre une diagonale ou un axe de symétrie peut révéler des informations importantes, notamment dans des parallélogrammes à angles droits ou non.
Les mesures d’un angle intérieur et la nature d’un trapèze rectangle permettent aussi de mieux classifier les types de quadrilatères selon leurs propriétés géométriques. Finalement, l’étude du quadrilatère de longueurs à travers les produits des longueurs de ses côtés opposés peut être une méthode complémentaire d’analyse.
Quiz sur les quadrilatères en maths
- Comment appelle-t-on un quadrilatère qui a quatre angles droits ?
- a) Trapèze
- b) Rectangle ✅
- c) Losange
Petit mot du lexique : « rectangle » vient du latin « rectus » qui signifie droit.
- Le losange a-t-il ses diagonales qui se coupent à angle droit (on dit qu’il est orthodiagonal) ?
- a) Oui ✅
- b) Non
- Parmi ces figures, laquelle est un polygone convexe ?
- a) Une étoile
- b) Un rectangle ✅
- c) Un croissant
- Comment s’appelle un cercle qui passe par tous les sommets d’un quadrilatère ?
- a) Cercle magique
- b) Cercle inscrit
- c) Cercle circonscrit ✅
Dans le langage mathématique, on dit que le quadrilatère est « circonscriptible ».